Rotation

As outlined in previos sections, a transformation is a combination of translation and rotation. In this section, the rotation part will be discussed.

In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation.1 Some examples:

  • Rotation matrices
  • Euler axis and angle
  • Euler rotations
  • Quarternions

In general, according to Euler's rotation theorem the rotation of a rigid body (or three-dimensional coordinate system with the fixed origin) is described by a single rotation about some axis. Such a rotation may be uniquely described by a minimum of three real parameters.1

Rotation formalisms

Rotation matrix

A 3x3 rotation matrix \({}^{A}_B R\) describes the rotation of the axes of coordinate system \(B\) relative to system \(A\).

The columns are formed from the three unit vectors of B's axes expressed in A: \({}^{A}\vec X_B\), \({}^{A}\vec Y_B\), and \({}^{A}\vec Z_B\).2

\[ {}^{A}_B R = \begin{bmatrix} {}^{A}\vec X_B & {}^{A}\vec Y_B & {}^{A}\vec Z_B \end{bmatrix} \]

An illustration of the 2-dimensional case can be found in Fig. 1. The unit vectors of the system B are expressed as vectors in system A:

\[ {}^{A}_B R = \begin{bmatrix} {}^{A}\vec X_B & {}^{A}\vec Y_B \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \]

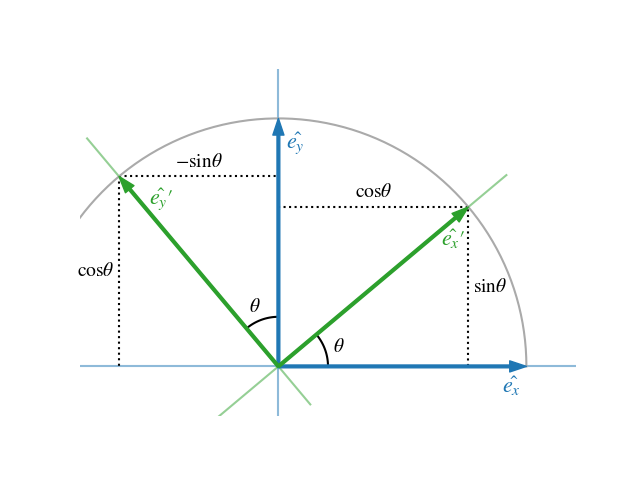
Figure 1: 2D rotation with a rotation angle \(\theta \)

The rotation matrix can be seen as a linear mapping between two coordinate systems:

\[ {}^{A}x = {}^{A}_B R \ {}^{B}x \]

Euler axis and angle

According to Euler's rotation theorem the rotation of a rigid body (or three-dimensional coordinate system with the fixed origin) is described by a single rotation about some axis. Such a rotation may be uniquely described by a minimum of three real parameters.1

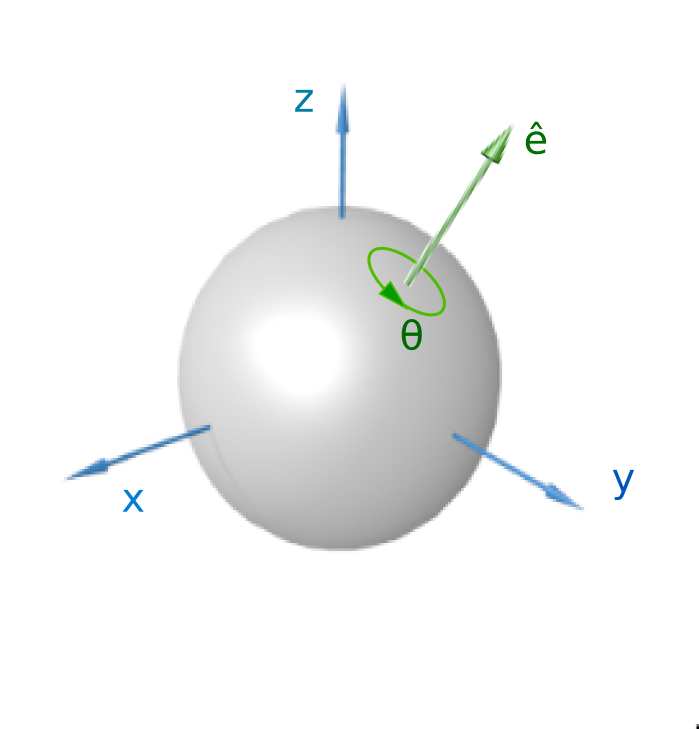
Figure 2: A visualization of a rotation represented by an Euler axis and angle. Image from 1

Euler rotations

The idea behind Euler rotations is to split the complete rotation of the coordinate system into three simpler constitutive rotations. That means, we can define a rotation by a chain of rotation axis and angels. The Euler rotations or Euler angles are also referred to as Davenport angles.

There are two groups, based on the order of the rotation axis:

  • Generalized (classical) Euler rotations: \( zxz, xyx, yzy, zyz, xzx, yxy \)
  • Generalized Tait–Bryan rotations: \( xyz, yzx, zxy, xzy, zyx, yxz \)

E.g. \( zxz \) is a rotation on the z-axis, followed by x and again z.

Note, that there is difference whether the rotation is applied intrinsically (i.e. the rotated axes is a starting point for the next rotation) or extrinsically (all the rotations are applied wrt. initial coordinates).

Note, that there are 24 (=2x(6+6)) ways in total to define a rotation.

Any extrinsic rotation is equivalent to an intrinsic rotation by the same angles but with inverted order of elemental rotations, and vice versa. For instance, the intrinsic rotations x-y-z by angles α, β, γ are equivalent to the extrinsic rotations z-y-x by angles γ, β, α.3 Both are represented by a rotation matrix R:

\[ R = R_x(\alpha) \ R_y(\beta) \ R_z(\gamma) \]

The formulas for the basic rotations (e.g. \( R_x(\alpha) \)) can be found here.

Quaternions

A quaternion representation of rotation is written as a versor (normalized quaternion):

\[ \hat{\mathbf{q}} =q_i\mathbf{i}+q_j\mathbf{j}+q_k\mathbf{k}+q_r = \begin{bmatrix} q_i \\ q_j \\ q_k \\ w \end{bmatrix} \]

A unit quaternion \(\mathbf q\) holds the information about the rotation axis \( [a_x, a_y, a_z]^T \) and the rotation angle \(\alpha\) (similar to Euler axis and angle representation):

\[ \mathbf q = sin(\frac \alpha 2) (a_x i + a_y j + a_z k) + cos(\frac \alpha 2) \\ q_i = sin(\frac \alpha 2) a_x i \\ q_j = sin(\frac \alpha 2) a_y j \\ q_k = sin(\frac \alpha 2) a_z k \\ w = cos(\frac \alpha 2) \]

Quaternions, which form a four-dimensional vector space, have proven very useful in representing & transmitting rotations due to several advantages over the other representations mentioned above.1 Quaternions are a very popular parametrization due to the following properties1:

  • More compact than the matrix representation (=less data to transmit and hold in memory) and less susceptible to round-off errors
  • Expression of the rotation matrix in terms of quaternion parameters involves no trigonometric functions (refer here) (=sin & cosinus are compute heavy)
  • It is simple to combine two individual rotations represented as quaternions using a quaternion product

References

1 Wikipedia - Rotation formalisms in three dimensions

3 Wikipedia - https://en.wikipedia.org/wiki/Davenport_chained_rotations