Basic datatypes
This chapter describes a collection of essential datatypes commonly used in the analysis technical entities such as vehicles or robots.
Point
A \( N \)-dimensional point is typically represented as a tuple of \( N \) floating point numbers:
# 3-dimensional point
p = (1.23, 342.2, 123.12)
In (geo-)spatial applications are usually used to represent a location. In general, a point can represent any entity (e.g. person in an employee) database as a tuple of its characteristics or features:
# 3-dimensional point
employee = (
31, # age [years]
5000, # monthly salary [$]
13, # time in the company [years]
)
Vector
A vector is geometric object which has a magnitude (length) and a direction.
The representation of a vector is equal to the points in the section above - you can define a vector by a tuple of \( N \) points.
Vectors are essential in technical domain. Forces, velocity, acceleration - all those terms are defined in terms of vectors:
# velocity vector of the rocket at start
v = (
0, # x [m/s]
0, # y [m/s]
7900.0, # z [m/s]
)
Lines
Line segment
In mathematics a line is an infinitely long object defined by a point and a vector. Alternatively we can define a line by two points. Since objects in our daily life are finite, we are dealing with line parts or segments, e.g. edges, sizes or paths.
A line segment can be represented with its end points \( p_0 \) and \( p_1 \). The length of the line segment is the magnitude of the direction vector \( ||\vec v ||_2 = || p_1 - p_0 ||_2 \).
Linestrings
Furthermore, multiple line segments can be combined to a polygonal chain. In computational geometry
and in many languages like Python or C#) polygonal chains are be referred to as LineStrings.
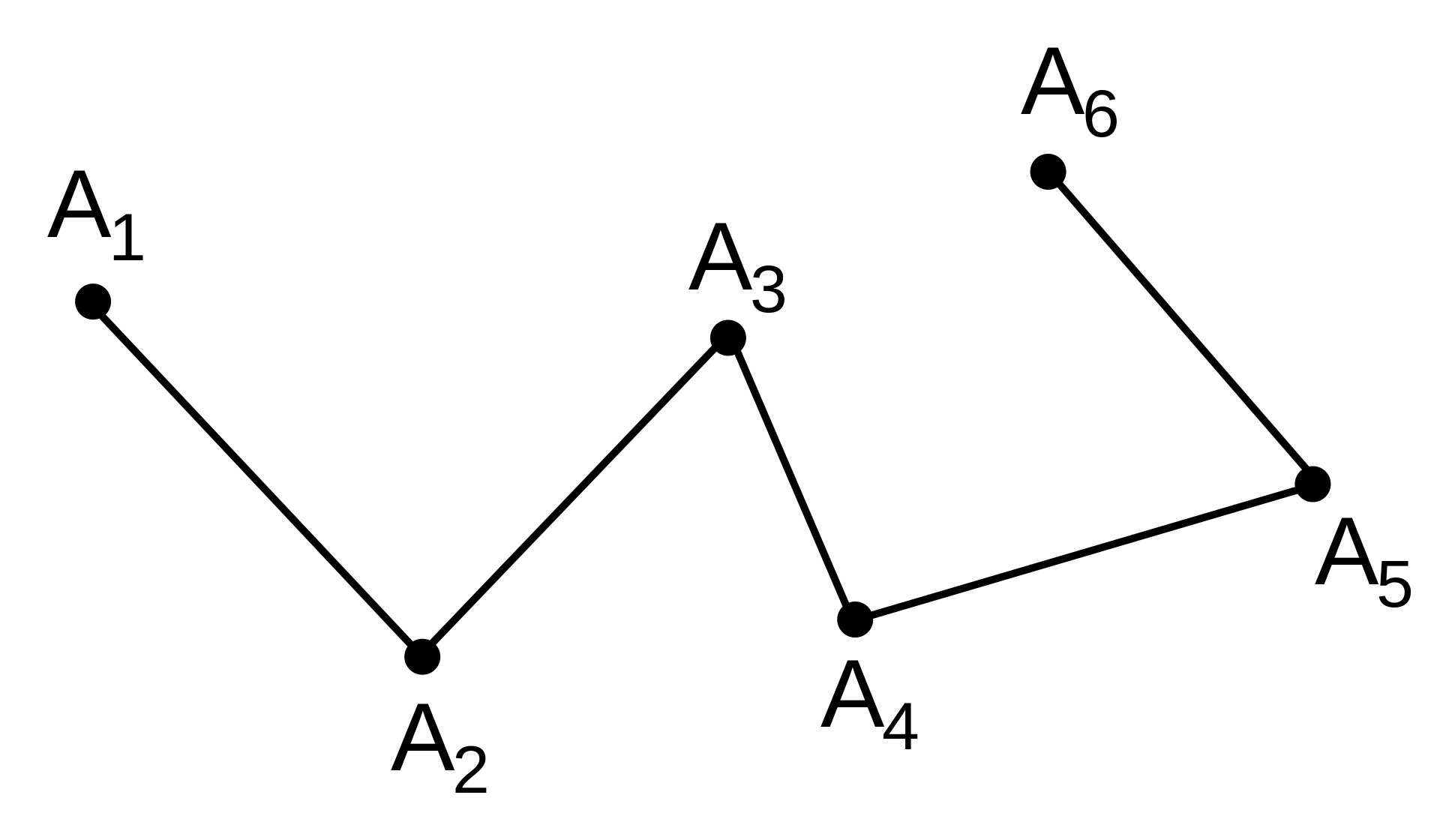
Figure 1: A linestring composed of 5 line segments. Image from Wikipedia.
Curves
It is not straightforward to define a curve in a single mathematically unique manner. In the following an example definition from Wikipedia:
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Curves can have multiple representations and combinations of the those representations.
Function graphs
A curve can be represented a a function, e.g. as a polynomial \( y = f(x) = c_3 x^3 + c_2 x^2 + c_1 x + c_0 \).
Figure 2: The graph of a polynomial function of degree 3. Image from Wikipedia.
Note that \( x \) is the independent variable. Defining circles in the function graph representation is not possible.
Topological path
A N-dimensional curve can be represented by its arc length \( s \in [0, 1] \) and a function in each dimension:
\[ p = \begin{bmatrix} f_x(s) \\ f_y(s) \\ f_z(s) \end{bmatrix} \]
Splines
A parametric spline is a composition of multiple topological paths, defined in a piece-wise manner.
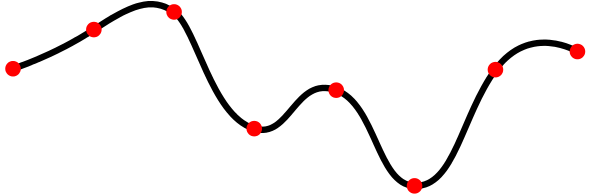
Figure 3: A spline with 8 knots, i.e. \( s \in [0, 7] \). Each section represents a topological path. Image from Wikipedia.
...
Note, that a 2D spline can be defined as a collection of multiple function graphs, where \( x \) is the independent variable. This has a more compact representation and less complex computation, but prevents to define circles or clothoids.
Clothoids (WIP)
Euler spirals ... WIP